When a ray of light passes at an angle from a less dense medium to a higher density medium, it is bent towards the normal (an imaginary line running at right angles to the surface between the mediums). This is referred to as refraction. The visible light from a heavenly body will be refracted when it enters the earth’s atmosphere. The amount of refraction will depend on the position of the body relative to the horizon. The maximum refraction will be experienced when the body is on the horizon. When the body is directly overhead, refraction will be zero.

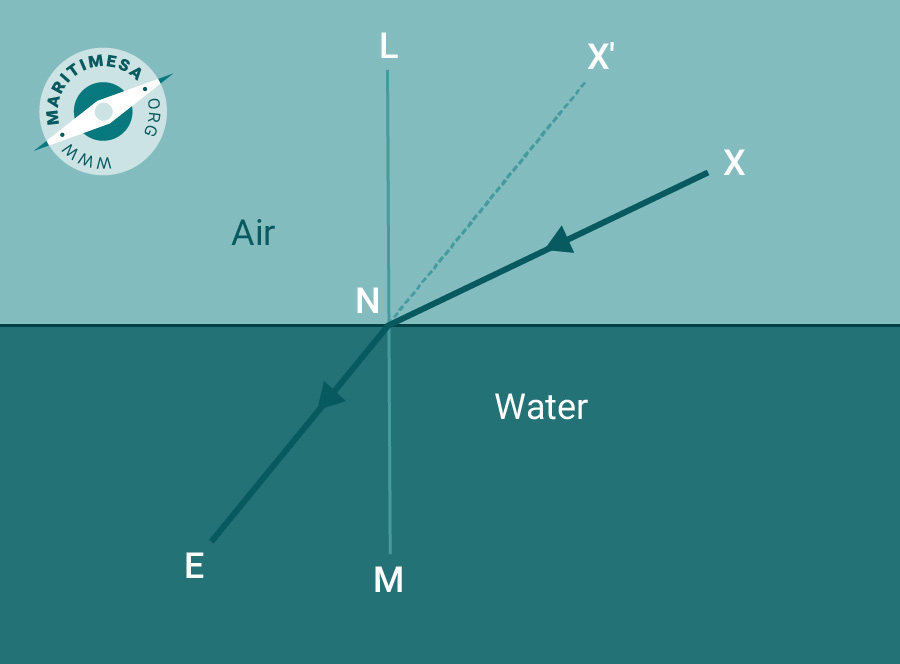
Refraction between air and water.

The density of the atmosphere is not uniform, but increases with altitude. The rays entering it will therefore be continuously bent as they approach the earth’s surface.  In other words the path of the rays would resemble a curve.

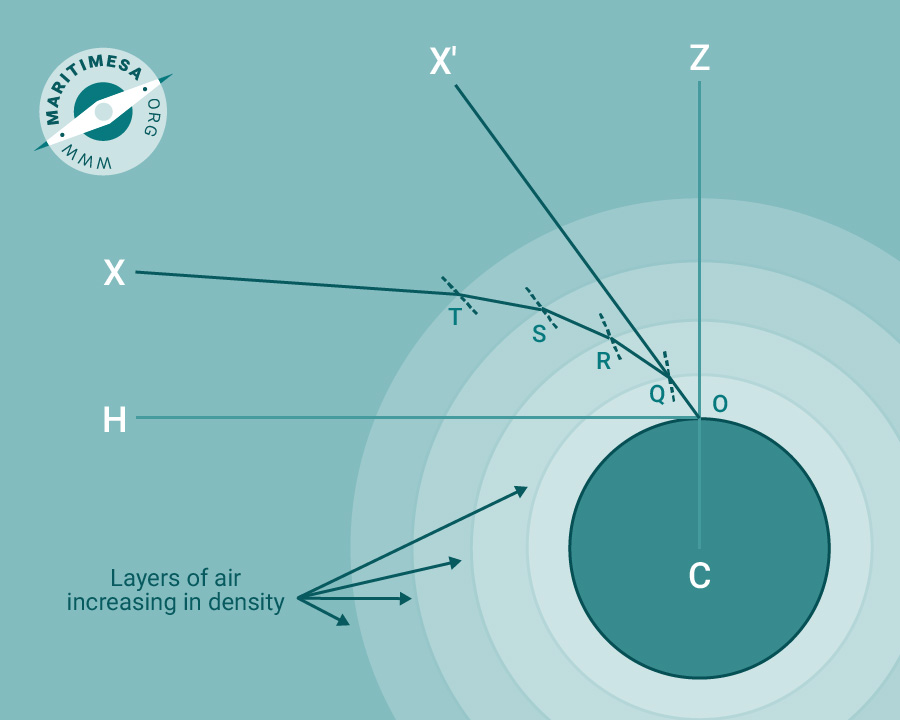
Atmospheric refraction.

Effect of refraction on dip.

Refraction not only appears to increase the altitude of a body but also changes the appearance of the horizon.  The horizon that one observes is not the one you would see if you drew a tangent from the observer’s eye to the earth’s surface.  If you did this, the horizon would be at T as indicated in the drawing.  But in reality what you would see is the horizon at T’.  Because the ray is bent as shown in the drawing, the visible horizon appears in the direction OD, where OD is tangent to T’O at O.  Dip is actually angle DOH, which is less than the theoretical angle of dip, TOH.  The Nautical Almanac gives the angle of Dip for heights of eye up to 48 metres.  The effect of refraction on the position of the horizon is included in the tabulated values of dip.

Effect of refraction on dip.