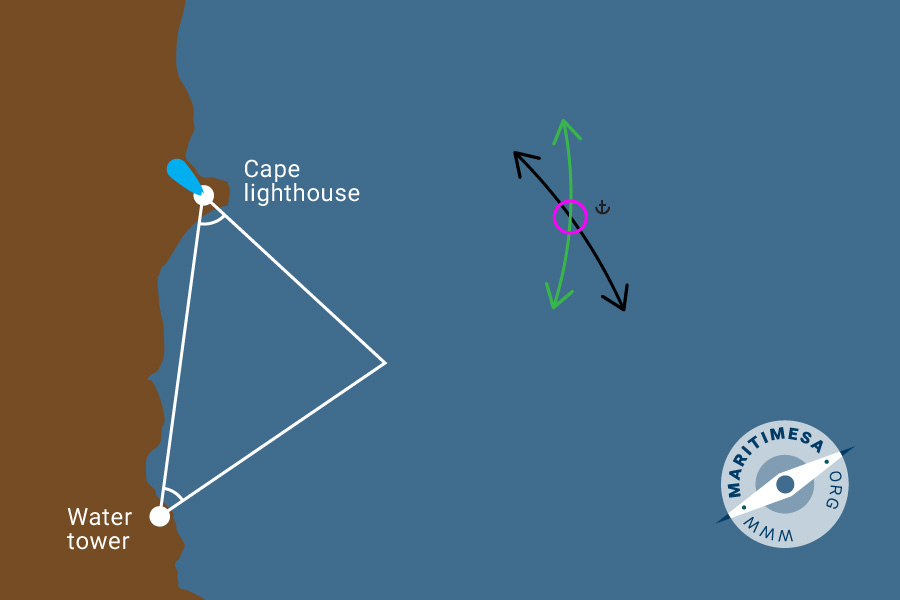
Problem:
Your vessel is anchored approximately 2 miles west of Cape Light. A horizontal sextant angle between the following points was taken:
Cape Light and the water tower south of the light = 65°

At the same time a vertical sextant angle was taken of Cape Light. The sextant reading was 0° 40.3’. The height of the light according to the chart is 70 metres.

Determine the position of the vessel.

Solution:
On the chart, join the positions of the light and the water tower and measure the bearing and its reciprocal between them.
On a note pad/book write down the bearings, ie

Calculate the base angle of the triangle to be constructed on the above line and write it below the above entry, ie

Calculate the intercept bearings for the centre of the position circle and enter them under the base angle calculation, ie.

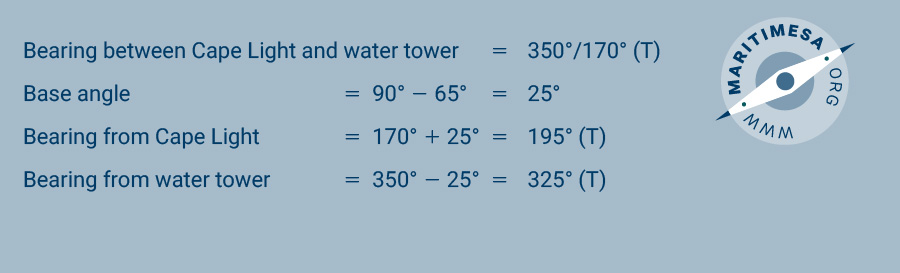
Plot the bearings obtained from the above on the chart.

Check the distance between each point and the intersect point. Since they are radii of the position circle they should be equal. Using these radii draw an arc of the position circle in the vicinity of the estimated anchor position.

In your note pad/book, write the formula for obtaining the distance from a vertical sextant angle (VSA). Substitute the values obtained from the sextant and the chart for the VSA and height of the observed object and calculate the distance, ie

Plot the arc of the position circle obtained from the above calculation. The position of the ship is where the two position circles intersect.